Skip to content

📈 RiskSim – Comprehensive Risk Simulation Framework

Monte Carlo, Historical, and Variance–Covariance Methods for Portfolio Risk Analysis

RiskSim is a Python-based risk analytics framework for quantitative portfolio risk estimation. It supports three major methodologies — Monte Carlo Simulation (Gaussian Copula), Historical Simulation, and the Variance–Covariance Method — within a unified and interactive environment.

The framework enables users to model portfolio dependencies, compute risk measures such as Value-at-Risk (VaR), Conditional VaR (CVaR), and the Power Spectral Risk Measure (PSRM), and analyze simulation stability via a modern Streamlit web interface.

👉 Check out on GitHub

Watch the video

🚀 Features

  • 🧠 Three Integrated Risk Methods

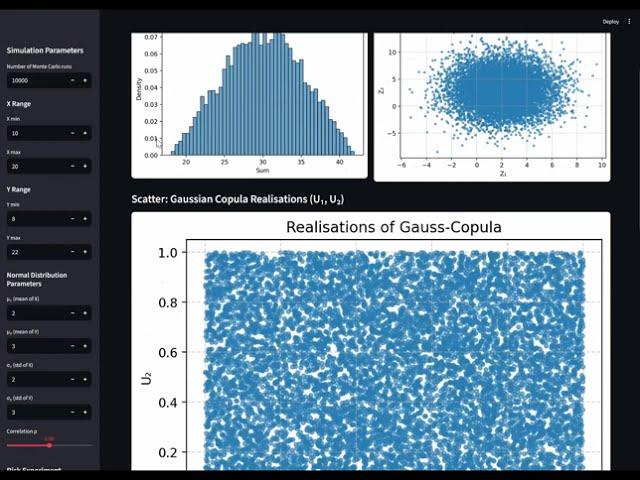
  • Monte Carlo Simulation (Gaussian Copula) – Generate correlated synthetic returns using the Gaussian copula.

  • Historical Simulation – Estimate risk directly from empirical portfolio return data.

  • Variance–Covariance Method – Compute risk measures under the normality assumption using μ–σ parameterization.

  • 📊 Risk Measure Computation – Compute VaR, CVaR, and PSRM across all methods.

  • 💻 Interactive Dashboard – Explore dependencies, distributions, and risk measure variability directly in your browser.

  • 🔁 Output Variability Demonstration – Check out the variability of Monte Carlo results under repeated sampling.

🧩 Methodological Overview

RiskSim provides three approaches to estimate portfolio risk.

1. Monte Carlo Simulation (Gaussian Copula)

The Monte Carlo method generates pseudo-random correlated realizations of portfolio components using a Gaussian copula. It allows flexible specification of marginal distributions and dependency structures via Cholesky decomposition of the covariance matrix.

Process Overview:

  1. Generate independent uniform random samples.
  2. Transform to standard normal variates.
  3. Introduce correlation using the covariance matrix.
  4. Convert to correlated uniform variables via the Gaussian copula.
  5. Apply user-defined marginals to obtain dependent portfolio returns.

This approach provides high flexibility for dependency modeling and portfolio stress testing.

2. Historical Simulation

The historical simulation approach uses observed empirical portfolio returns instead of simulated data. Each asset’s historical returns are combined to form portfolio returns and used directly to calculate VaR, CVaR, and PSRM without any distributional assumptions. This method reflects real-world market behavior, capturing skewness, kurtosis, and tail effects inherent in empirical data.

3. Variance–Covariance (Parametric) Method

This analytical method assumes normally distributed returns, parameterized by mean (μ) and standard deviation (σ). A variance–covariance matrix models interdependencies between assets.

Computation:

  • Portfolio variance is derived analytically from the covariance matrix.
  • Portfolio losses are computed under normality assumptions.
  • VaR, CVaR, and PSRM are evaluated using the parameterized results.

🧮 High-Level Process

  1. Variable Specification – Define simulation parameters (means, standard deviations, correlations, sample sizes).
  2. Covariance & Cholesky Decomposition – Construct correlation structures for dependent random variables.
  3. Portfolio Return Generation – Depending on the chosen method, generate simulated, empirical, or analytical portfolio return data.
  4. Risk Measure Estimation – Calculate VaR, CVaR, and PSRM consistently across all methods.
  5. Visualization & Analysis – Explore dependencies, distributions, and stability effects through interactive charts.

📉 Risk Measure Computation

RiskSim provides three core risk measures, applicable across Monte Carlo, Historical, and Variance–Covariance methods.

1. Value-at-Risk (VaR)

VaR represents the α-quantile of the portfolio loss distribution, i.e., the loss that is not exceeded with probability (1 − α).

Historical Simulation:

  • Portfolio realizations are sorted ascendingly into RM_list.
  • The quantile index is alpha * len(RM_list), yielding the VaR cutoff.

Variance–Covariance:

  • Computed analogously, but using analytically parameterized portfolio returns from var_covar_results.

Monte Carlo:

  • Derived from simulated portfolio distributions produced by the copula-based generator.

2. Conditional Value-at-Risk (CVaR)

CVaR is the mean loss beyond the VaR threshold.

Procedure:

  1. Identify all losses up to the α-quantile in RM_list.
  2. Store them in CVaR_list.
  3. Compute their arithmetic mean to estimate the CVaR.

3. Power Spectral Risk Measure (PSRM)

A nonlinear risk measure introducing subjective probability weighting:

\[\Phi_b(p) = b \cdot p^{b-1}, \quad p \in [0,1], ; b \in (0,1)\]

Conceptual Steps:

  1. Sort portfolio losses into RM_list.
  2. Compute subjective probability weights subj_ws_list as:
\[w_i = \left(\frac{i}{N}\right)^\gamma - \left(\frac{i-1}{N}\right)^\gamma\]
  1. The expected return is the mean of RM_list.
  2. The power-spectral risk is the matrix product of the transposed RM_list and subj_ws_list.

Smaller γ values emphasize tail events, while larger ones distribute weight more evenly.

▶️ Run the Streamlit Application

1. Clone the repository

git clone https://github.com/trholy/risksim.git
cd risksim

2. Build and run Docker container

docker-compose up --build

3. Access in browser: http://localhost:8501

📂 Project Structure

risksim
├── .dockerignore
├── .gitignore
├── Dockerfile
├── LICENSE
├── README.md
├── datasets
├── docker-compose.yml
├── pyproject.toml
├── setup.py
├── src
│   └── risksim
│       ├── __init__.py
│       ├── copula
│       │   └── copula.py
│       ├── experiment
│       │   └── experiment.py
│       ├── plot
│       │   └── plotting.py
│       ├── risk
│       │   └── risk.py
│       └── utils
│           └── utils.py
└── streamlit-app
    ├── app.py
    └── requirements.txt

📜 License

This project is released under the MIT License. You are free to use, modify, and distribute it with proper attribution.